Python 实现的选择排序
选择排序
选择排序(Selection Sort)算法会查找数组中的最低值,并将其移动到数组的开头。
{{ msgDone }}
该算法会反复遍历数组,将接下来的最低值移动到数组前端,直到数组排序完成。
工作原理:
- 遍历数组以查找最低值。
- 将最低值移动到数组未排序部分的开头。
- 根据数组中的值的数量,再次遍历数组。
手动运行示例
在 Python 程序中实现选择排序算法之前,让我们先手动对一个短数组仅运行一次,以了解其原理。
第 1 步:从未排序数组开始。
[ 7, 12, 9, 11, 3]
第 2 步:逐个遍历数组。哪个值最低?3,对吧?
[ 7, 12, 9, 11, 3]
第 3 步:将最低值 3 移动到数组开头。
[ 3, 7, 12, 9, 11]
第 4 步:从 7 开始查看剩余值。7 是最低值,并且已经在数组开头,因此我们无需移动它。
[ 3, 7, 12, 9, 11]
第 5 步:查看数组剩余部分:12、9 和 11。9 是最低值。
[ 3, 7, 12, 9, 11]
第 6 步:将 9 移动到开头。
[ 3, 7, 9, 12, 11]
第 7 步:查看 12 和 11,11 是最低值。
[ 3, 7, 9, 12, 11]
第 8 步:将其移动到开头。
[ 3, 7, 9, 11, 12]
最终,数组已排序。
运行下面的模拟,以动画形式查看上述步骤:
在 Python 中实现选择排序
要在 Python 中实现选择排序算法,我们需要:
- 待排序的数组。
- 内部循环,用于遍历数组,查找最低值,并将其移动到数组开头。每次运行时,此循环必须遍历的值数量减少一个。
- 外部循环,用于控制内部循环的运行次数。对于包含 \(n\) 个值的数组,此外部循环必须运行 \(n-1\) 次。
生成的代码如下所示:
实例
在 Python 列表上使用选择排序:
mylist = [64, 34, 25, 5, 22, 11, 90, 12]
n = len(mylist)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if mylist[j] < mylist[min_index]:
min_index = j
min_value = mylist.pop(min_index)
mylist.insert(i, min_value)
print(mylist)
选择排序的移动问题
选择排序算法还可以进一步改进。
在上面的代码中,最低值元素被移除,然后插入到数组开头。
每次移除下一个最低值数组元素时,所有后续元素都必须向下移动一个位置,以弥补移除操作。
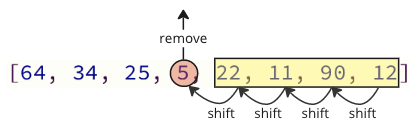
这些移动操作非常耗时,而且我们甚至还没有完成!在找到并移除最低值(5)后,将其插入到数组开头,导致所有后续值向上移动一个位置,为新值腾出空间,如下面的图像所示。
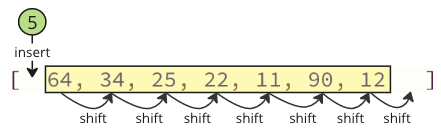
注意:如果使用 Python 或 Java 等高级编程语言,在代码中不会看到这些移动操作,但这些移动操作仍在后台进行。此类移动操作需要计算机花费额外时间来完成,这可能会成为问题。
解决方案:交换值!
无需进行所有移动操作,只需像下面这样将最低值(5)与第一个值(64)交换即可。

我们可以像上面的图像所示那样交换值,因为最低值最终会处于正确位置,而且我们将要与之交换的另一个值放在哪里都无所谓,因为它尚未排序。
以下是一个模拟,展示了这种改进后的带交换操作的选择排序的工作原理:
{{ msgDone }}
我们将在选择排序算法中插入改进:
实例
改进后的选择排序算法,包括交换值:
mylist = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(mylist)
for i in range(n):
min_index = i
for j in range(i+1, n):
if mylist[j] < mylist[min_index]:
min_index = j
mylist[i], mylist[min_index] = mylist[min_index], mylist[i]
print(mylist)
选择排序的时间复杂度
选择排序对包含 \(n\) 个值的数组进行排序。
平均而言,在每个循环中需要比较大约 \(\frac{n}{2}\) 个元素才能找到最低值。
而且选择排序必须运行循环来查找最低值大约 \(n\) 次。
我们得到时间复杂度:\( O( \frac{n}{2} \cdot n) = {O(n^2)} \)。
选择排序算法的时间复杂度可以用如下图形展示:
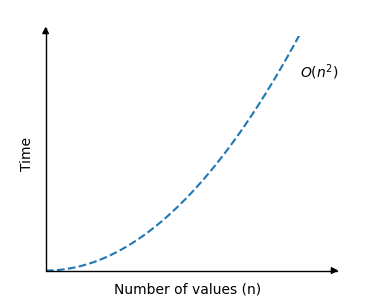
如你所见,运行时间与冒泡排序相同:当数组大小增加时,运行时间会迅速增加。