Python 实现的 DSA 计数排序

计数排序

计数排序算法通过计算每个值出现的次数来对数组进行排序。

运行模拟程序，查看如何使用计数排序对从 1 到 5 的 17 个整数值进行排序。

与之前研究的排序算法不同，计数排序不比较值，且仅适用于非负整数。

此外，当可能值的范围 \(k\) 小于值的数量 \(n\) 时，计数排序的速度很快。

计数排序的条件

计数排序据说仅适用于有限范围内的非负整数值，原因如下：

• 整数值：计数排序依赖于统计不同值的出现次数，因此这些值必须是整数。对于整数，每个值都对应一个索引（对于非负值），且不同值的数量有限，因此可能的不同值数量 \(k\) 与值的数量 \(n\) 相比不会太大。
• 非负值：计数排序通常通过创建一个计数数组来实现。当算法遍历要排序的值时，值 x 通过增加索引 x 处的计数数组值来进行计数。如果我们尝试对负值进行排序，那么在排序值 -3 时就会遇到问题，因为索引 -3 将在计数数组之外。
• 有限的值范围：如果要排序的可能不同值的数量 \(k\) 大于要排序的值的数量 \(n\)，则我们用于排序的计数数组将比需要排序的原始数组大，从而使算法变得无效。

手动运行

在编程语言中实现计数排序算法之前，让我们先手动对一个短数组进行排序，以便理解其原理。

第 1 步：我们从一个未排序的数组开始。

myArray = [ 2, 3, 0, 2, 3, 2]

第 2 步：我们创建另一个数组来统计每个值的数量。该数组有 4 个元素，用于存储 0 到 3 的值。

myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 0, 0]

第 3 步：现在开始计数。第一个元素是 2，因此我们必须增加索引 2 处的计数数组元素。

myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 0]

第 4 步：统计完一个值后，我们可以将其移除，并统计下一个值，即 3。

myArray = [ 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 1]

第 5 步：我们要统计的下一个值是 0，因此我们增加计数数组中索引 0 的值。

myArray = [ 0, 2, 3, 2]
countArray = [ 1, 0, 1, 1]

第 6 步：我们继续这样操作，直到所有值都被统计。

myArray = [ ]
countArray = [ 1, 0, 3, 2]

第 7 步：现在我们将根据初始数组重新创建元素，并按从低到高的顺序排列它们。

计数数组中的第一个元素告诉我们有 1 个值为 0 的元素。因此，我们将 1 个值为 0 的元素推入数组，并将计数数组中索引 0 处的元素减 1。

myArray = [ 0]
countArray = [ 0, 0, 3, 2]

第 8 步：从计数数组中我们可以看出，不需要创建任何值为 1 的元素。

myArray = [ 0]
countArray = [ 0, 0, 3, 2]

第 9 步：我们将 3 个值为 2 的元素推入数组末尾。在创建这些元素时，我们还将索引 2 处的计数数组减 1。

myArray = [ 0, 2, 2, 2]
countArray = [ 0, 0, 0, 2]

第 10 步：最后，我们必须在数组末尾添加 2 个值为 3 的元素。

myArray = [0, 2, 2, 2, 3, 3]
countArray = [ 0, 0, 0, 0]

终于完成了！数组已排序。

运行下面的模拟程序，查看上述步骤的动画演示：

在 Python 中实现计数排序

要在 Python 程序中实现计数排序算法，我们需要：

1. 包含待排序值的数组。
2. countingSort 方法，接收一个整数数组。
3. 方法内部的一个数组，用于统计值的数量。
4. 方法内部的一个循环，通过增加计数数组中的元素来统计并移除值。
5. 方法内部的另一个循环，使用计数数组重新创建数组，使元素按正确顺序排列。

还有一件事：我们需要找出数组中的最高值，以便创建正确大小的计数数组。例如，如果最高值是 5，则计数数组必须总共有 6 个元素，以便能够统计所有可能的非负整数 0、1、2、3、4 和 5。

生成的代码如下所示：

实例

在 Python 程序中使用计数排序算法：

def countingSort(arr):
  max_val = max(arr)
  count = [0] * (max_val + 1)

  while len(arr) > 0:
    num = arr.pop(0)
    count[num] += 1

  for i in range(len(count)):
    while count[i] > 0:
      arr.append(i)
      count[i] -= 1

  return arr

mylist = [4, 2, 2, 6, 3, 3, 1, 6, 5, 2, 3]
mysortedlist = countingSort(mylist)
print(mysortedlist)

亲自试一试

计数排序时间复杂度

计数排序算法的运行速度取决于可能值的范围 \(k\) 和值的数量 \(n\)。

一般来说，计数排序的时间复杂度为 \(O(n+k)\)。

在最佳情况下，可能的不同值范围 \(k\) 与值的数量 \(n\) 相比非常小，此时计数排序的时间复杂度为 \(O(n)\)。

但在最坏情况下，可能的不同值范围 \(k\) 与值的数量 \(n\) 相比非常大，此时计数排序的时间复杂度可能达到 \(O(n^2)\) 甚至更糟。

下图显示了计数排序的时间复杂度可能有多大差异。

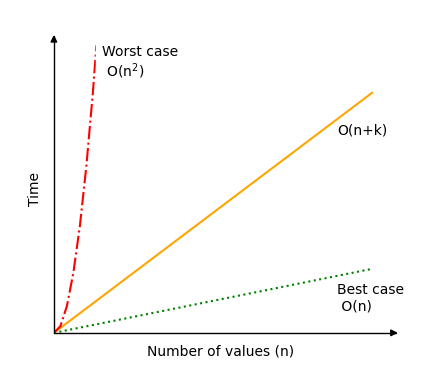
如您所见，在选择计数排序作为算法之前，考虑值的范围与要排序的值的数量之间的关系非常重要。此外，如本页顶部所述，请记住计数排序仅适用于非负整数值。

如前所述：如果要排序的数字在值上差异很大（大的 \(k\)），且要排序的数字很少（小的 \(n\)），则计数排序算法无效。

如果我们固定 \(n\) 和 \(k\)，则上述模拟中的“随机”、“降序”和“升序”选项产生的操作次数相同。这是因为在所有三种情况下都会发生相同的事情：设置计数数组、统计数字并创建新的已排序数组。