Python е®һзҺ°зҡ„дәҢеҲҶжҹҘжүҫ
дәҢеҲҶжҹҘжүҫ
дәҢеҲҶжҹҘжүҫз®—жі•еңЁе·ІжҺ’еәҸж•°з»„дёӯиҝӣиЎҢжҗңзҙўпјҢ并иҝ”еӣһе…¶жҗңзҙўеҖјжүҖеңЁзҡ„зҙўеј•гҖӮ
{{ msgDone }}
иҝҗиЎҢжЁЎжӢҹпјҢжҹҘзңӢдәҢеҲҶжҹҘжүҫз®—жі•зҡ„е·ҘдҪңеҺҹзҗҶгҖӮ
дәҢеҲҶжҹҘжүҫжҜ”зәҝжҖ§жҹҘжүҫеҝ«еҫ—еӨҡпјҢдҪҶиҰҒжұӮж•°з»„е·ІжҺ’еәҸжүҚиғҪе·ҘдҪңгҖӮ
дәҢеҲҶжҹҘжүҫз®—жі•йҖҡиҝҮжЈҖжҹҘж•°з»„дёӯй—ҙдҪҚзҪ®зҡ„еҖјжқҘе·ҘдҪңгҖӮеҰӮжһңзӣ®ж ҮеҖјиҫғдҪҺпјҢеҲҷдёӢдёҖдёӘиҰҒжЈҖжҹҘзҡ„еҖјдҪҚдәҺж•°з»„е·ҰеҚҠйғЁеҲҶзҡ„дёӯй—ҙдҪҚзҪ®гҖӮиҝҷз§Қжҗңзҙўж–№ејҸж„Ҹе‘ізқҖжҗңзҙўеҢәеҹҹе§Ӣз»ҲжҳҜеүҚдёҖдёӘжҗңзҙўеҢәеҹҹзҡ„дёҖеҚҠпјҢеӣ жӯӨдәҢеҲҶжҹҘжүҫз®—жі•зҡ„йҖҹеәҰйқһеёёеҝ«гҖӮ
жҗңзҙўеҢәеҹҹеҮҸеҚҠзҡ„иҝҮзЁӢдјҡдёҖзӣҙжҢҒз»ӯпјҢзӣҙеҲ°жүҫеҲ°зӣ®ж ҮеҖјпјҢжҲ–иҖ…зӣҙеҲ°ж•°з»„зҡ„жҗңзҙўеҢәеҹҹдёәз©әгҖӮ
е·ҘдҪңеҺҹзҗҶпјҡ
- жЈҖжҹҘж•°з»„дёӯй—ҙдҪҚзҪ®зҡ„еҖјгҖӮ
- еҰӮжһңзӣ®ж ҮеҖјиҫғдҪҺпјҢеҲҷжҗңзҙўж•°з»„зҡ„е·ҰеҚҠйғЁеҲҶгҖӮеҰӮжһңзӣ®ж ҮеҖјиҫғй«ҳпјҢеҲҷжҗңзҙўеҸіеҚҠйғЁеҲҶгҖӮ
- еҜ№ж•°з»„ж–°зҡ„зј©е°ҸйғЁеҲҶ继з»ӯжү§иЎҢжӯҘйӘӨ 1 е’Ң 2пјҢзӣҙеҲ°жүҫеҲ°зӣ®ж ҮеҖјжҲ–жҗңзҙўеҢәеҹҹдёәз©әгҖӮ
- еҰӮжһңжүҫеҲ°иҜҘеҖјпјҢеҲҷиҝ”еӣһзӣ®ж ҮеҖјзҡ„зҙўеј•гҖӮеҰӮжһңжңӘжүҫеҲ°зӣ®ж ҮеҖјпјҢеҲҷиҝ”еӣһ -1гҖӮ
жүӢеҠЁиҝҗиЎҢзӨәдҫӢ
и®©жҲ‘们е°қиҜ•жүӢеҠЁиҝӣиЎҢжҗңзҙўпјҢд»ҘдҫҝеңЁе®һйҷ…еңЁPythonзЁӢеәҸдёӯе®һзҺ°дәҢеҲҶжҹҘжүҫд№ӢеүҚпјҢжӣҙеҘҪең°дәҶи§Је…¶е·ҘдҪңеҺҹзҗҶгҖӮжҲ‘们е°ҶжҗңзҙўеҖј 11гҖӮ
第 1 жӯҘпјҡжҲ‘们д»ҺдёҖдёӘж•°з»„ејҖе§ӢгҖӮ
[ 2, 3, 7, 7, 11, 15, 25]
第 2 жӯҘпјҡж•°з»„дёӯй—ҙзҙўеј• 3 еӨ„зҡ„еҖјжҳҜеҗҰзӯүдәҺ 11пјҹ
[ 2, 3, 7, 7, 11, 15, 25]
第 3 жӯҘпјҡ7 е°ҸдәҺ 11пјҢеӣ жӯӨжҲ‘们еҝ…йЎ»еңЁзҙўеј• 3 зҡ„еҸідҫ§жҗңзҙў 11гҖӮзҙўеј• 3 еҸідҫ§зҡ„еҖјдёә [ 11, 15, 25]гҖӮдёӢдёҖдёӘиҰҒжЈҖжҹҘзҡ„еҖјжҳҜзҙўеј• 5 еӨ„зҡ„дёӯй—ҙеҖј 15гҖӮ
[ 2, 3, 7, 7, 11, 15, 25]
第 4 жӯҘпјҡ15 й«ҳдәҺ 11пјҢеӣ жӯӨжҲ‘们еҝ…йЎ»еңЁзҙўеј• 5 зҡ„е·Ұдҫ§жҗңзҙўгҖӮжҲ‘们已з»ҸжЈҖжҹҘдәҶзҙўеј• 0-3пјҢеӣ жӯӨеҸӘеү©дёӢзҙўеј• 4 йңҖиҰҒжЈҖжҹҘгҖӮ
[ 2, 3, 7, 7, 11, 15, 25]
жҲ‘们жүҫеҲ°дәҶе®ғпјҒ
еҖј 11 дҪҚдәҺзҙўеј• 4гҖӮ
иҝ”еӣһзҙўеј•дҪҚзҪ® 4гҖӮ
дәҢеҲҶжҹҘжүҫз»“жқҹгҖӮ
иҝҗиЎҢдёӢйқўзҡ„жЁЎжӢҹпјҢжҹҘзңӢдёҠиҝ°жӯҘйӘӨзҡ„еҠЁз”»жј”зӨәпјҡ
еңЁ Python дёӯе®һзҺ°дәҢеҲҶжҹҘжүҫ
иҰҒе®һзҺ°дәҢеҲҶжҹҘжүҫз®—жі•пјҢжҲ‘们йңҖиҰҒпјҡ
- еҢ…еҗ«еҫ…жҗңзҙўеҖјзҡ„ж•°з»„гҖӮ
- иҰҒжҗңзҙўзҡ„зӣ®ж ҮеҖјгҖӮ
- еҫӘзҺҜпјҢеҸӘиҰҒе·Ұзҙўеј•е°ҸдәҺжҲ–зӯүдәҺеҸізҙўеј•е°ұ继з»ӯиҝҗиЎҢгҖӮ
- if иҜӯеҸҘпјҢз”ЁдәҺжҜ”иҫғдёӯй—ҙеҖјдёҺзӣ®ж ҮеҖјпјҢеҰӮжһңжүҫеҲ°зӣ®ж ҮеҖјеҲҷиҝ”еӣһзҙўеј•гҖӮ
- if иҜӯеҸҘпјҢз”ЁдәҺжЈҖжҹҘзӣ®ж ҮеҖјжҳҜе°ҸдәҺиҝҳжҳҜеӨ§дәҺдёӯй—ҙеҖјпјҢ并жӣҙж–°вҖңе·ҰвҖқжҲ–вҖңеҸівҖқеҸҳйҮҸд»Ҙзј©е°ҸжҗңзҙўеҢәеҹҹгҖӮ
- еҫӘзҺҜз»“жқҹеҗҺпјҢиҝ”еӣһ -1пјҢеӣ дёәжӯӨж—¶жҲ‘们зҹҘйҒ“жңӘжүҫеҲ°зӣ®ж ҮеҖјгҖӮ
дәҢеҲҶжҹҘжүҫзҡ„жңҖз»Ҳд»Јз ҒеҰӮдёӢжүҖзӨәпјҡ
е®һдҫӢ
еңЁ Python дёӯеҲӣе»әдәҢеҲҶжҹҘжүҫз®—жі•пјҡ
def binarySearch(arr, targetVal):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == targetVal:
return mid
if arr[mid] < targetVal:
left = mid + 1
else:
right = mid - 1
return -1
mylist = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
x = 11
result = binarySearch(mylist, x)
if result != -1:
print("Found at index", result)
else:
print("Not found")
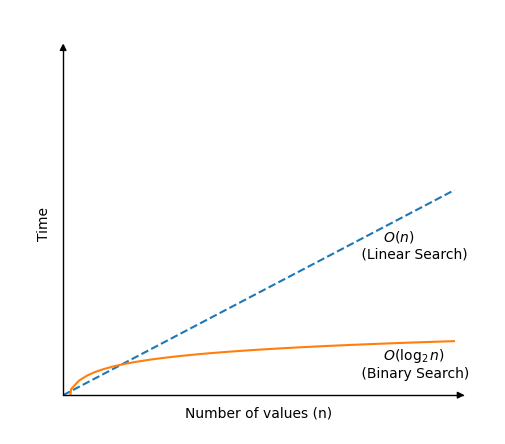
дәҢеҲҶжҹҘжүҫж—¶й—ҙеӨҚжқӮеәҰ
жҜҸж¬ЎдәҢеҲҶжҹҘжүҫжЈҖжҹҘдёҖдёӘж–°еҖјд»ҘжҹҘзңӢе…¶жҳҜеҗҰдёәзӣ®ж ҮеҖјж—¶пјҢжҗңзҙўеҢәеҹҹйғҪдјҡеҮҸеҚҠгҖӮ
иҝҷж„Ҹе‘ізқҖпјҢеҚідҪҝеңЁдәҢеҲҶжҹҘжүҫж— жі•жүҫеҲ°зӣ®ж ҮеҖјзҡ„жңҖеқҸжғ…еҶөдёӢпјҢе®ғд»Қ然еҸӘйңҖиҰҒ \( \log_{2}n \) ж¬ЎжҜ”иҫғеҚіеҸҜйҒҚеҺҶеҢ…еҗ« \(n\) дёӘеҖјзҡ„е·ІжҺ’еәҸж•°з»„гҖӮ
дәҢеҲҶжҹҘжүҫзҡ„ж—¶й—ҙеӨҚжқӮеәҰдёәпјҡ\( O( \log_{2} n ) \)
жіЁж„ҸпјҡдҪҝз”ЁеӨ§ O иЎЁзӨәжі•иЎЁзӨәж—¶й—ҙеӨҚжқӮеәҰж—¶пјҢжҲ‘们д№ҹеҸҜд»ҘеҸӘеҶҷ \( O( \log n ) \)пјҢдҪҶ \( O( \log_{2} n ) \) жҸҗйҶ’жҲ‘们пјҢжҜҸж¬Ўж–°жҜ”иҫғйғҪдјҡе°Ҷж•°з»„жҗңзҙўеҢәеҹҹеҮҸеҚҠпјҢиҝҷжҳҜдәҢеҲҶжҹҘжүҫзҡ„еҹәжң¬жҰӮеҝөпјҢеӣ жӯӨеңЁиҝҷз§Қжғ…еҶөдёӢпјҢжҲ‘们е°Ҷдҝқз•ҷд»Ҙ 2 дёәеә•ж•°зҡ„иЎЁзӨәжі•гҖӮ
еҰӮжһңжҲ‘们з»ҳеҲ¶дәҢеҲҶжҹҘжүҫеңЁеҢ…еҗ« \(n\) дёӘеҖјзҡ„ж•°з»„дёӯжҹҘжүҫжҹҗдёӘеҖјжүҖйңҖзҡ„ж—¶й—ҙеӣҫпјҢ并дёҺзәҝжҖ§жҹҘжүҫиҝӣиЎҢжҜ”иҫғпјҢе°Ҷеҫ—еҲ°дёӢеӣҫпјҡ