Python е®һзҺ°зҡ„жҸ’е…ҘжҺ’еәҸ
жҸ’е…ҘжҺ’еәҸ
жҸ’е…ҘжҺ’еәҸпјҲInsertion Sortпјүз®—жі•дҪҝз”Ёж•°з»„зҡ„дёҖйғЁеҲҶжқҘеӯҳж”ҫе·ІжҺ’еәҸзҡ„еҖјпјҢеҸҰдёҖйғЁеҲҶжқҘеӯҳж”ҫе°ҡжңӘжҺ’еәҸзҡ„еҖјгҖӮ
{{ msgDone }}
иҜҘз®—жі•жҜҸж¬Ўд»Һж•°з»„жңӘжҺ’еәҸзҡ„йғЁеҲҶдёӯеҸ–еҮәдёҖдёӘеҖјпјҢ并е°Ҷе…¶ж”ҫе…Ҙе·ІжҺ’еәҸйғЁеҲҶзҡ„жӯЈзЎ®дҪҚзҪ®пјҢзӣҙеҲ°ж•°з»„жҺ’еәҸе®ҢжҲҗгҖӮ
е·ҘдҪңеҺҹзҗҶпјҡ
- д»Һж•°з»„жңӘжҺ’еәҸзҡ„йғЁеҲҶдёӯеҸ–еҮә第дёҖдёӘеҖјгҖӮ
- е°ҶиҜҘеҖјз§»еҠЁеҲ°ж•°з»„е·ІжҺ’еәҸйғЁеҲҶзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮ
- ж №жҚ®жңӘжҺ’еәҸйғЁеҲҶдёӯеҖјзҡ„ж•°йҮҸпјҢеҶҚж¬ЎйҒҚеҺҶж•°з»„жңӘжҺ’еәҸйғЁеҲҶгҖӮ
жүӢеҠЁиҝҗиЎҢзӨәдҫӢ
еңЁ Python зЁӢеәҸдёӯе®һзҺ°жҸ’е…ҘжҺ’еәҸз®—жі•д№ӢеүҚпјҢи®©жҲ‘们е…ҲжүӢеҠЁеҜ№дёҖдёӘзҹӯж•°з»„иҝӣиЎҢжҺ’еәҸпјҢд»ҘдәҶи§Је…¶еҺҹзҗҶгҖӮ
第 1 жӯҘпјҡд»ҺжңӘжҺ’еәҸж•°з»„ејҖе§ӢгҖӮ
[ 7, 12, 9, 11, 3]
第 2 жӯҘпјҡжҲ‘们еҸҜд»Ҙе°Ҷ第дёҖдёӘеҖји§Ҷдёәж•°з»„е·ІжҺ’еәҸйғЁеҲҶзҡ„еҲқе§ӢеҖјгҖӮеҰӮжһңеҸӘжңүдёҖдёӘеҖјпјҢйӮЈд№Ҳе®ғдёҖе®ҡжҳҜе·ІжҺ’еәҸзҡ„пјҢеҜ№еҗ§пјҹ
[ 7, 12, 9, 11, 3]
第 3 жӯҘпјҡзҺ°еңЁпјҢдёӢдёҖдёӘеҖј 12 еә”移еҠЁеҲ°ж•°з»„е·ІжҺ’еәҸйғЁеҲҶзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮдҪҶжҳҜ 12 еӨ§дәҺ 7пјҢеӣ жӯӨе®ғе·Із»ҸеңЁжӯЈзЎ®зҡ„дҪҚзҪ®гҖӮ
[ 7, 12, 9, 11, 3]
第 4 жӯҘпјҡиҖғиҷ‘дёӢдёҖдёӘеҖј 9гҖӮ
[ 7, 12, 9, 11, 3]
第 5 жӯҘпјҡзҺ°еңЁпјҢеҖј 9 еҝ…须移еҠЁеҲ°ж•°з»„е·ІжҺ’еәҸйғЁеҲҶзҡ„жӯЈзЎ®дҪҚзҪ®пјҢеӣ жӯӨжҲ‘们е°Ҷ 9 移еҠЁеҲ° 7 е’Ң 12 д№Ӣй—ҙгҖӮ
[ 7, 9, 12, 11, 3]
第 6 жӯҘпјҡдёӢдёҖдёӘеҖјжҳҜ 11гҖӮ
[ 7, 9, 12, > 11, 3]
第 7 жӯҘпјҡжҲ‘们е°Ҷ其移еҠЁеҲ°ж•°з»„е·ІжҺ’еәҸйғЁеҲҶзҡ„ 9 е’Ң 12 д№Ӣй—ҙгҖӮ
[ 7, 9, 11, 12, 3]
第 8 жӯҘпјҡжңҖеҗҺдёҖдёӘиҰҒжҸ’е…ҘеҲ°жӯЈзЎ®дҪҚзҪ®зҡ„еҖјжҳҜ 3гҖӮ
[ 7, 9, 11, 12, 3]
第 9 жӯҘпјҡжҲ‘们е°Ҷ 3 жҸ’е…ҘеҲ°жүҖжңүе…¶д»–еҖјд№ӢеүҚпјҢеӣ дёәе®ғжҳҜжңҖдҪҺеҖјгҖӮ
[ 3, 7, 9, 11, 12]
жңҖз»ҲпјҢж•°з»„е·ІжҺ’еәҸгҖӮ
иҝҗиЎҢдёӢйқўзҡ„жЁЎжӢҹпјҢд»ҘеҠЁз”»еҪўејҸжҹҘзңӢдёҠиҝ°жӯҘйӘӨпјҡ
еңЁ Python дёӯе®һзҺ°жҸ’е…ҘжҺ’еәҸ
иҰҒеңЁ Python зЁӢеәҸдёӯе®һзҺ°жҸ’е…ҘжҺ’еәҸз®—жі•пјҢжҲ‘们йңҖиҰҒпјҡ
- еҫ…жҺ’еәҸзҡ„ж•°з»„гҖӮ
- еӨ–йғЁеҫӘзҺҜпјҢз”ЁдәҺйҖүжӢ©дёҖдёӘиҰҒжҺ’еәҸзҡ„еҖјгҖӮеҜ№дәҺеҢ…еҗ« \(n\) дёӘеҖјзҡ„ж•°з»„пјҢжӯӨеӨ–йғЁеҫӘзҺҜи·іиҝҮ第дёҖдёӘеҖјпјҢ并且еҝ…йЎ»иҝҗиЎҢ \(n-1\) ж¬ЎгҖӮ
- еҶ…йғЁеҫӘзҺҜпјҢз”ЁдәҺйҒҚеҺҶж•°з»„зҡ„е·ІжҺ’еәҸйғЁеҲҶпјҢд»ҘжүҫеҲ°жҸ’е…ҘеҖјзҡ„дҪҚзҪ®гҖӮеҰӮжһңиҰҒжҺ’еәҸзҡ„еҖјдҪҚдәҺзҙўеј• \(i\) еӨ„пјҢеҲҷж•°з»„зҡ„е·ІжҺ’еәҸйғЁеҲҶд»Һзҙўеј• \(0\) ејҖе§ӢпјҢеҲ°зҙўеј• \(i-1\) з»“жқҹгҖӮ
з”ҹжҲҗзҡ„д»Јз ҒеҰӮдёӢжүҖзӨәпјҡ
е®һдҫӢ
еңЁ Python еҲ—иЎЁдёҠдҪҝз”ЁжҸ’е…ҘжҺ’еәҸпјҡ
mylist = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(mylist)
for i in range(1,n):
insert_index = i
current_value = mylist.pop(i)
for j in range(i-1, -1, -1):
if mylist[j] > current_value:
insert_index = j
mylist.insert(insert_index, current_value)
print(mylist)
жҸ’е…ҘжҺ’еәҸзҡ„ж”№иҝӣ
жҸ’е…ҘжҺ’еәҸиҝҳеҸҜд»ҘиҝӣдёҖжӯҘж”№иҝӣгҖӮ
дёҠиҝ°д»Јз ҒйҰ–е…Ҳ移йҷӨдёҖдёӘеҖјпјҢ然еҗҺе°Ҷе…¶жҸ’е…ҘеҲ°е…¶д»–дҪҚзҪ®пјҢиҝҷз§Қж–№жі•еҫҲзӣҙи§ӮгҖӮдҫӢеҰӮпјҢеҰӮжһңдҪ з”ЁжүӢдёӯзҡ„дёҖеүҜзүҢиҝӣиЎҢжҸ’е…ҘжҺ’еәҸпјҢе°ұдјҡиҝҷж ·еҒҡгҖӮеҰӮжһңдҪҺеҖјзүҢе·ІжҺ’еәҸеҲ°е·Ұдҫ§пјҢдҪ дјҡжӢҝиө·дёҖеј ж–°зҡ„жңӘжҺ’еәҸзүҢпјҢ并е°Ҷе…¶жҸ’е…ҘеҲ°е…¶д»–е·ІжҺ’еәҸзүҢд№Ӣй—ҙзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮ
д»Ҙиҝҷз§Қж–№ејҸзј–зЁӢзҡ„й—®йўҳеңЁдәҺпјҢеҪ“д»Һж•°з»„дёӯ移йҷӨдёҖдёӘеҖјж—¶пјҢжүҖжңүдёҠж–№зҡ„е…ғзҙ йғҪеҝ…йЎ»еҗ‘дёӢ移еҠЁдёҖдёӘзҙўеј•дҪҚзҪ®пјҡ
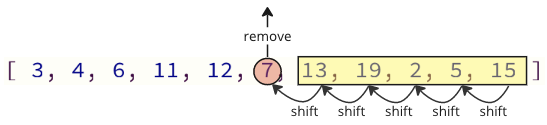
并且пјҢеҪ“е°Ҷ移йҷӨзҡ„еҖјеҶҚж¬ЎжҸ’е…ҘеҲ°ж•°з»„дёӯж—¶пјҢиҝҳеҝ…йЎ»иҝӣиЎҢи®ёеӨҡ移еҠЁж“ҚдҪңпјҡжүҖжңүеҗҺз»ӯе…ғзҙ йғҪеҝ…йЎ»еҗ‘дёҠ移еҠЁдёҖдёӘдҪҚзҪ®пјҢд»ҘдҫҝдёәжҸ’е…Ҙзҡ„еҖји…ҫеҮәз©әй—ҙпјҡ
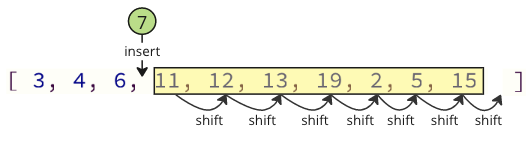
иҝҷдәӣ移еҠЁж“ҚдҪңеҸҜиғҪдјҡиҠұиҙ№еӨ§йҮҸж—¶й—ҙпјҢе°Өе…¶жҳҜеҜ№дәҺеҢ…еҗ«и®ёеӨҡе…ғзҙ зҡ„ж•°з»„гҖӮ
йҡҗи—Ҹзҡ„еҶ…еӯҳ移еҠЁпјҡеҰӮжһңдҪҝз”Ё Python жҲ– JavaScript зӯүй«ҳзә§зј–зЁӢиҜӯиЁҖпјҢеңЁд»Јз ҒдёӯдёҚдјҡзңӢеҲ°иҝҷдәӣ移еҠЁж“ҚдҪңпјҢдҪҶиҝҷдәӣ移еҠЁж“ҚдҪңд»ҚеңЁеҗҺеҸ°иҝӣиЎҢгҖӮжӯӨзұ»з§»еҠЁж“ҚдҪңйңҖиҰҒи®Ўз®—жңәиҠұиҙ№йўқеӨ–ж—¶й—ҙжқҘе®ҢжҲҗпјҢиҝҷеҸҜиғҪдјҡжҲҗдёәй—®йўҳгҖӮ
дҪ еҸҜд»ҘеңЁжӯӨеӨ„дәҶи§Јжңүе…іж•°з»„еңЁеҶ…еӯҳдёӯеӯҳеӮЁж–№ејҸзҡ„жӣҙеӨҡдҝЎжҒҜгҖӮ
ж”№иҝӣж–№жЎҲ
жҲ‘们еҸҜд»ҘйҖҡиҝҮ仅移еҠЁеҝ…иҰҒзҡ„еҖјжқҘйҒҝе…ҚеӨ§еӨҡж•°иҝҷдәӣ移еҠЁж“ҚдҪңпјҡ
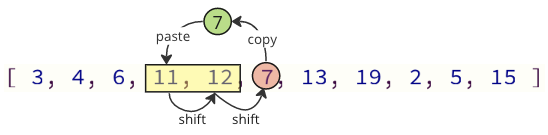
еңЁдёҠйқўзҡ„еӣҫеғҸдёӯпјҢйҰ–е…ҲеӨҚеҲ¶еҖј 7пјҢ然еҗҺе°ҶеҖј 11 е’Ң 12 еңЁж•°з»„дёӯеҗ‘дёҠ移еҠЁдёҖдёӘдҪҚзҪ®пјҢжңҖеҗҺе°ҶеҖј 7 ж”ҫеңЁеҖј 11 д№ӢеүҚзҡ„дҪҚзҪ®гҖӮ
еңЁиҝҷз§Қжғ…еҶөдёӢпјҢ移еҠЁж“ҚдҪңзҡ„ж•°йҮҸд»Һ 12 еҮҸе°‘еҲ° 2гҖӮ
дёӢйқўзҡ„зӨәдҫӢе®һзҺ°дәҶиҝҷдёҖж”№иҝӣпјҡ
е®һдҫӢ
еңЁжҺ’еәҸз®—жі•дёӯжҸ’е…Ҙж”№иҝӣпјҡ
mylist = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(mylist)
for i in range(1,n):
insert_index = i
current_value = mylist[i]
for j in range(i-1, -1, -1):
if mylist[j] > current_value:
mylist[j+1] = mylist[j]
insert_index = j
else:
break
mylist[insert_index] = current_value
print(mylist)
дёҠиҝ°д»Јз ҒдёӯиҝҳеҒҡдәҶеҸҰдёҖ件дәӢпјҢеҚіи·іеҮәеҶ…йғЁеҫӘзҺҜгҖӮиҝҷжҳҜеӣ дёәеҪ“жҲ‘们已з»ҸдёәеҪ“еүҚеҖјжүҫеҲ°жӯЈзЎ®зҡ„дҪҚзҪ®ж—¶пјҢе°ұжІЎжңүеҝ…иҰҒ继з»ӯжҜ”иҫғеҖјдәҶгҖӮ
жҸ’е…ҘжҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰ
жҸ’е…ҘжҺ’еәҸеҜ№еҢ…еҗ« \(n\) дёӘеҖјзҡ„ж•°з»„иҝӣиЎҢжҺ’еәҸгҖӮ
е№іеқҮиҖҢиЁҖпјҢжҜҸдёӘеҖјеҝ…йЎ»дёҺе…¶д»–еӨ§зәҰ \(\frac{n}{2}\) дёӘеҖјиҝӣиЎҢжҜ”иҫғпјҢд»ҘжүҫеҲ°жҸ’е…Ҙзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮ
жҸ’е…ҘжҺ’еәҸеҝ…йЎ»иҝҗиЎҢеҫӘзҺҜжқҘе°ҶеҖјжҸ’е…ҘеҲ°е…¶жӯЈзЎ®дҪҚзҪ®еӨ§зәҰ \(n\) ж¬ЎгҖӮ
жҲ‘们еҫ—еҲ°жҸ’е…ҘжҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰпјҡ\( O( \frac{n}{2} \cdot n) = {O(n^2)} \)гҖӮ
жҸ’е…ҘжҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰеҸҜд»ҘеҰӮдёӢжүҖзӨәпјҡ
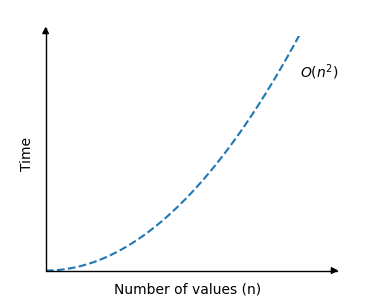
еҜ№дәҺжҸ’е…ҘжҺ’еәҸпјҢжңҖдҪігҖҒе№іеқҮе’ҢжңҖеқҸжғ…еҶөеңәжҷҜд№Ӣй—ҙеӯҳеңЁеҫҲеӨ§е·®ејӮгҖӮ
жҺҘдёӢжқҘжҳҜеҝ«йҖҹжҺ’еәҸгҖӮжңҖеҗҺпјҢжҲ‘们е°ҶзңӢеҲ°дёҖдёӘжӣҙеҝ«зҡ„жҺ’еәҸз®—жі•пјҒ