Python е®һзҺ°зҡ„ DSA еҝ«йҖҹжҺ’еәҸ
еҝ«йҖҹжҺ’еәҸ
йЎҫеҗҚжҖқд№үпјҢеҝ«йҖҹжҺ’еәҸжҳҜжңҖеҝ«зҡ„жҺ’еәҸз®—жі•д№ӢдёҖгҖӮ
еҝ«йҖҹжҺ’еәҸз®—жі•еҸ–дёҖдёӘеҖјж•°з»„пјҢйҖүжӢ©е…¶дёӯдёҖдёӘеҖјдҪңдёәвҖңжһўиҪҙвҖқе…ғзҙ пјҢ并移еҠЁе…¶д»–еҖјпјҢдҪҝиҫғе°Ҹзҡ„еҖјдҪҚдәҺжһўиҪҙе…ғзҙ зҡ„е·Ұдҫ§пјҢиҫғеӨ§зҡ„еҖјдҪҚдәҺе…¶еҸідҫ§гҖӮ
{{ msgDone }}
еңЁжң¬ж•ҷзЁӢдёӯпјҢжҲ‘们йҖүжӢ©ж•°з»„зҡ„жңҖеҗҺдёҖдёӘе…ғзҙ дҪңдёәжһўиҪҙе…ғзҙ пјҢдҪҶжҲ‘们д№ҹеҸҜд»ҘйҖүжӢ©ж•°з»„зҡ„第дёҖдёӘе…ғзҙ пјҢжҲ–иҖ…ж•°з»„дёӯзҡ„д»»ж„Ҹе…ғзҙ гҖӮ
然еҗҺпјҢеҝ«йҖҹжҺ’еәҸз®—жі•еҜ№жһўиҪҙе…ғзҙ е·ҰеҸідёӨдҫ§зҡ„еӯҗж•°з»„йҖ’еҪ’ең°жү§иЎҢзӣёеҗҢзҡ„ж“ҚдҪңгҖӮиҝҷдёҖиҝҮзЁӢжҢҒз»ӯеҲ°ж•°з»„жҺ’еәҸе®ҢжҲҗгҖӮ
йҖ’еҪ’жҳҜжҢҮеҮҪж•°и°ғз”ЁиҮӘиә«гҖӮ
еңЁеҝ«йҖҹжҺ’еәҸз®—жі•е°ҶжһўиҪҙе…ғзҙ зҪ®дәҺе·Ұдҫ§дёәиҫғе°ҸеҖјеӯҗж•°з»„гҖҒеҸідҫ§дёәиҫғеӨ§еҖјеӯҗж•°з»„д№Ӣй—ҙеҗҺпјҢиҜҘз®—жі•дјҡи°ғз”ЁиҮӘиә«дёӨж¬ЎпјҢд»Ҙдҫҝеҝ«йҖҹжҺ’еәҸеҶҚж¬ЎеҜ№е·Ұдҫ§еӯҗж•°з»„е’ҢеҸідҫ§еӯҗж•°з»„иҝҗиЎҢгҖӮеҝ«йҖҹжҺ’еәҸз®—жі•дјҡжҢҒз»ӯи°ғз”ЁиҮӘиә«пјҢзӣҙеҲ°еӯҗж•°з»„еӨӘе°ҸиҖҢж— жі•жҺ’еәҸгҖӮ
иҜҘз®—жі•зҡ„жҸҸиҝ°еҰӮдёӢпјҡ
е·ҘдҪңеҺҹзҗҶпјҡ
- йҖүжӢ©ж•°з»„дёӯзҡ„дёҖдёӘеҖјдҪңдёәжһўиҪҙе…ғзҙ гҖӮ
- еҜ№ж•°з»„зҡ„е…¶дҪҷйғЁеҲҶиҝӣиЎҢжҺ’еәҸпјҢдҪҝе°ҸдәҺжһўиҪҙе…ғзҙ зҡ„еҖјдҪҚдәҺе·Ұдҫ§пјҢиҫғеӨ§зҡ„еҖјдҪҚдәҺеҸідҫ§гҖӮ
- е°ҶжһўиҪҙе…ғзҙ дёҺиҫғеӨ§еҖјзҡ„第дёҖдёӘе…ғзҙ дәӨжҚўпјҢдҪҝжһўиҪҙе…ғзҙ дҪҚдәҺиҫғе°ҸеҖје’ҢиҫғеӨ§еҖјд№Ӣй—ҙгҖӮ
- еҜ№жһўиҪҙе…ғзҙ е·ҰеҸідёӨдҫ§зҡ„еӯҗж•°з»„жү§иЎҢзӣёеҗҢзҡ„ж“ҚдҪңпјҲйҖ’еҪ’пјүгҖӮ
жүӢеҠЁиҝҗиЎҢ
еңЁзј–зЁӢиҜӯиЁҖдёӯе®һзҺ°еҝ«йҖҹжҺ’еәҸз®—жі•д№ӢеүҚпјҢи®©жҲ‘们е…ҲжүӢеҠЁеҜ№дёҖдёӘзҹӯж•°з»„иҝӣиЎҢжҺ’еәҸпјҢд»ҘдҫҝзҗҶи§Је…¶еҺҹзҗҶгҖӮ
第 1 жӯҘпјҡжҲ‘们д»ҺдёҖдёӘжңӘжҺ’еәҸзҡ„ж•°з»„ејҖе§ӢгҖӮ
[ 11, 9, 12, 7, 3]
第 2 жӯҘпјҡжҲ‘们йҖүжӢ©жңҖеҗҺдёҖдёӘеҖј 3 дҪңдёәжһўиҪҙе…ғзҙ гҖӮ
[ 11, 9, 12, 7, 3]
第 3 жӯҘпјҡж•°з»„дёӯзҡ„е…¶дҪҷеҖјйғҪеӨ§дәҺ 3пјҢеҝ…йЎ»дҪҚдәҺ 3 зҡ„еҸідҫ§гҖӮе°Ҷ 3 дёҺ 11 дәӨжҚўгҖӮ
[ 3, 9, 12, 7, 11]
第 4 жӯҘпјҡеҖј 3 зҺ°еңЁеӨ„дәҺжӯЈзЎ®зҡ„дҪҚзҪ®гҖӮжҲ‘们йңҖиҰҒеҜ№ 3 еҸідҫ§зҡ„еҖјиҝӣиЎҢжҺ’еәҸгҖӮжҲ‘们йҖүжӢ©жңҖеҗҺдёҖдёӘеҖј 11 дҪңдёәж–°зҡ„жһўиҪҙе…ғзҙ гҖӮ
[ 3, 9, 12, 7, 11]
第 5 жӯҘпјҡеҖј 7 еҝ…йЎ»дҪҚдәҺжһўиҪҙеҖј 11 зҡ„е·Ұдҫ§пјҢиҖҢ 12 еҝ…йЎ»дҪҚдәҺе…¶еҸідҫ§гҖӮ移еҠЁ 7 е’Ң 12гҖӮ
[ 3, 9, 7, 12, 11]
第 6 жӯҘпјҡе°Ҷ 11 дёҺ 12 дәӨжҚўпјҢдҪҝиҫғе°Ҹзҡ„еҖј 9 е’Ң 7 дҪҚдәҺ 11 зҡ„е·Ұдҫ§пјҢиҖҢ 12 дҪҚдәҺе…¶еҸідҫ§гҖӮ
[ 3, 9, 7, 11, 12]
第 7 жӯҘпјҡ11 е’Ң 12 еӨ„дәҺжӯЈзЎ®зҡ„дҪҚзҪ®гҖӮжҲ‘们еңЁ 11 е·Ұдҫ§зҡ„еӯҗж•°з»„ [ 9, 7] дёӯйҖүжӢ© 7 дҪңдёәжһўиҪҙе…ғзҙ гҖӮ
[ 3, 9, 7, 11, 12]
第 8 жӯҘпјҡжҲ‘们еҝ…йЎ»е°Ҷ 9 дёҺ 7 дәӨжҚўгҖӮ
[ 3, 7, 9, 11, 12]
зҺ°еңЁпјҢж•°з»„е·ІжҺ’еәҸе®ҢжҲҗгҖӮ
иҝҗиЎҢдёӢйқўзҡ„жЁЎжӢҹзЁӢеәҸпјҢжҹҘзңӢдёҠиҝ°жӯҘйӘӨзҡ„еҠЁз”»жј”зӨәпјҡ
еңЁ Python дёӯе®һзҺ°еҝ«йҖҹжҺ’еәҸ
иҰҒзј–еҶҷдёҖдёӘиғҪеӨҹе°Ҷж•°з»„дёҚж–ӯеҲҶеүІдёәжӣҙе°Ҹеӯҗж•°з»„зҡ„ 'quickSort' ж–№жі•пјҢжҲ‘们йңҖиҰҒдҪҝз”ЁйҖ’еҪ’жҠҖжңҜгҖӮиҝҷж„Ҹе‘ізқҖ 'quickSort' ж–№жі•еҝ…йЎ»иғҪеӨҹиҮӘжҲ‘и°ғз”ЁпјҢеҲҶеҲ«еӨ„зҗҶеҹәеҮҶе…ғзҙ е·Ұдҫ§е’ҢеҸідҫ§зҡ„ж–°еӯҗж•°з»„гҖӮзӮ№еҮ»жӯӨеӨ„дәҶи§ЈжӣҙеӨҡе…ідәҺйҖ’еҪ’зҡ„зҹҘиҜҶгҖӮ
иҰҒеңЁ Python зЁӢеәҸдёӯе®һзҺ°еҝ«йҖҹжҺ’еәҸз®—жі•пјҢжҲ‘们йңҖиҰҒпјҡ
- еҫ…жҺ’еәҸзҡ„еҖјж•°з»„
- иғҪиҮӘжҲ‘и°ғз”Ёзҡ„ quickSort ж–№жі•пјҲйҖ’еҪ’пјүпјҢеҪ“еӯҗж•°з»„й•ҝеәҰеӨ§дәҺ 1 时继з»ӯеҲҶеүІ
partitionж–№жі•пјҢз”ЁдәҺжҺҘ收еӯҗж•°з»„гҖҒи°ғж•ҙе…ғзҙ дҪҚзҪ®гҖҒе°ҶеҹәеҮҶе…ғзҙ дәӨжҚўеҲ°жӯЈзЎ®дҪҚзҪ®пјҢ并иҝ”еӣһдёӢдёҖж¬Ўеӯҗж•°з»„еҲҶеүІзҡ„зҙўеј•дҪҚзҪ®
жңҖз»Ҳе®һзҺ°зҡ„д»Јз ҒеҰӮдёӢпјҡ
е®һдҫӢ
еңЁ Python зЁӢеәҸдёӯдҪҝз”Ёеҝ«йҖҹжҺ’еәҸз®—жі•пјҡ
def partition(array, low, high):
pivot = array[high]
i = low - 1
for j in range(low, high):
if array[j] <= pivot:
i += 1
array[i], array[j] = array[j], array[i]
array[i+1], array[high] = array[high], array[i+1]
return i+1
def quicksort(array, low=0, high=None):
if high is None:
high = len(array) - 1
if low < high:
pivot_index = partition(array, low, high)
quicksort(array, low, pivot_index-1)
quicksort(array, pivot_index+1, high)
mylist = [64, 34, 25, 5, 22, 11, 90, 12]
quicksort(mylist)
print(mylist)
еҝ«йҖҹжҺ’еәҸж—¶й—ҙеӨҚжқӮеәҰ
еҝ«йҖҹжҺ’еәҸзҡ„жңҖеқҸжғ…еҶөжҳҜ \(O(n^2) \)гҖӮиҝҷжҳҜжҢҮеңЁжҜҸдёӘеӯҗж•°з»„дёӯпјҢжһўиҪҙе…ғзҙ иҰҒд№ҲжҳҜжңҖй«ҳеҖјпјҢиҰҒд№ҲжҳҜжңҖдҪҺеҖјпјҢиҝҷдјҡеҜјиҮҙеӨ§йҮҸзҡ„йҖ’еҪ’и°ғз”ЁгҖӮеҜ№дәҺжҲ‘们дёҠйқўзҡ„е®һзҺ°пјҢеҪ“ж•°з»„е·Із»ҸжҺ’еәҸж—¶пјҢе°ұдјҡеҮәзҺ°иҝҷз§Қжғ…еҶөгҖӮ
дҪҶе№іеқҮиҖҢиЁҖпјҢеҝ«йҖҹжҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰе®һйҷ…дёҠеҸӘжңү \(O(n \log n) \)пјҢиҝҷжҜ”жҲ‘们д№ӢеүҚз ”з©¶иҝҮзҡ„е…¶д»–жҺ’еәҸз®—жі•иҰҒеҘҪеҫ—еӨҡгҖӮиҝҷе°ұжҳҜеҝ«йҖҹжҺ’еәҸеҰӮжӯӨеҸ—ж¬ўиҝҺзҡ„еҺҹеӣ гҖӮ
еңЁдёӢж–ҮдёӯпјҢжӮЁеҸҜд»ҘзңӢеҲ°еңЁе№іеқҮжғ…еҶөдёӢпјҢеҝ«йҖҹжҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰ \(O(n \log n) \) зӣёжҜ”д№ӢеүҚзҡ„ж—¶й—ҙеӨҚжқӮеәҰдёә \(O(n^2) \) зҡ„еҶ’жіЎжҺ’еәҸгҖҒйҖүжӢ©жҺ’еәҸе’ҢжҸ’е…ҘжҺ’еәҸз®—жі•жңүдәҶжҳҫи‘—ж”№е–„пјҡ
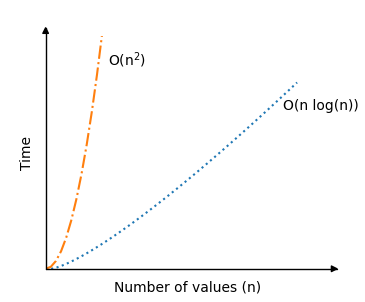
еҝ«йҖҹжҺ’еәҸз®—жі•зҡ„йҖ’еҪ’йғЁеҲҶе®һйҷ…дёҠжҳҜе№іеқҮжҺ’еәҸеңәжҷҜеҰӮжӯӨд№Ӣеҝ«зҡ„еҺҹеӣ пјҢеӣ дёәеҜ№дәҺжһўиҪҙе…ғзҙ зҡ„иүҜеҘҪйҖүжӢ©пјҢжҜҸж¬Ўз®—жі•и°ғз”ЁиҮӘиә«ж—¶пјҢж•°з»„йғҪдјҡеӨ§иҮҙеқҮеҢҖең°еҲҶжҲҗдёӨеҚҠгҖӮеӣ жӯӨпјҢеҚідҪҝеҖјж•°йҮҸ n зҝ»еҖҚпјҢйҖ’еҪ’и°ғз”Ёзҡ„ж¬Ўж•°д№ҹдёҚдјҡзҝ»еҖҚгҖӮ