Python е®һзҺ°зҡ„ DSA еҹәж•°жҺ’еәҸ
еҹәж•°жҺ’еәҸ
еҹәж•°жҺ’еәҸз®—жі•йҖҡиҝҮйҖҗдёӘеӨ„зҗҶж•°еӯ—зҡ„еҗ„дёӘдҪҚж•°пјҲд»ҺжңҖдҪҺжңүж•ҲдҪҚпјҢеҚіжңҖеҸіиҫ№зҡ„ж•°еӯ—ејҖе§ӢпјүжқҘеҜ№ж•°з»„иҝӣиЎҢжҺ’еәҸгҖӮ
зӮ№еҮ»жҢүй’®пјҢжҜҸж¬ЎеҜ№дёҖдёӘдҪҚж•°пјҲж•°еӯ—пјүиҝӣиЎҢеҹәж•°жҺ’еәҸгҖӮ
еҚ•еҮ»жҢүй’®йҖҗжӯҘпјҲжҢүдҪҚпјүжү§иЎҢеҹәж•°жҺ’еәҸгҖӮ
{{ msgDone }}еҹәж•°пјҲжҲ–еә•ж•°пјүжҳҜж•°еӯ—зі»з»ҹдёӯе”ҜдёҖж•°еӯ—зҡ„ж•°йҮҸгҖӮеңЁйҖҡеёёдҪҝз”Ёзҡ„еҚҒиҝӣеҲ¶зі»з»ҹдёӯпјҢжңү 10 дёӘдёҚеҗҢзҡ„ж•°еӯ—пјҢд»Һ 0 еҲ° 9гҖӮ
еҹәж•°жҺ’еәҸеҲ©з”Ёеҹәж•°пјҢе°ҶеҚҒиҝӣеҲ¶еҖјж”ҫе…Ҙ 10 дёӘдёҚеҗҢзҡ„жЎ¶пјҲжҲ–е®№еҷЁпјүдёӯпјҢиҝҷдәӣжЎ¶еҜ№еә”дәҺеҪ“еүҚе…іжіЁзҡ„ж•°еӯ—пјҢ然еҗҺеңЁеӨ„зҗҶдёӢдёҖдёӘж•°еӯ—д№ӢеүҚе°Ҷе®ғ们ж”ҫеӣһж•°з»„гҖӮ
еҹәж•°жҺ’еәҸжҳҜдёҖз§ҚйқһжҜ”иҫғз®—жі•пјҢд»…йҖӮз”ЁдәҺйқһиҙҹж•ҙж•°гҖӮ
еҹәж•°жҺ’еәҸз®—жі•еҸҜд»Ҙиҝҷж ·жҸҸиҝ°пјҡ
е·ҘдҪңеҺҹзҗҶпјҡ
- д»ҺжңҖдҪҺжңүж•ҲдҪҚпјҲжңҖеҸіиҫ№зҡ„ж•°еӯ—пјүејҖе§ӢгҖӮ
- ж №жҚ®еҪ“еүҚе…іжіЁзҡ„ж•°еӯ—еҜ№еҖјиҝӣиЎҢжҺ’еәҸпјҢйҰ–е…Ҳж №жҚ®еҪ“еүҚе…іжіЁзҡ„ж•°еӯ—е°ҶеҖјж”ҫе…ҘжӯЈзЎ®зҡ„жЎ¶дёӯпјҢ然еҗҺд»ҘжӯЈзЎ®йЎәеәҸе°Ҷе®ғ们ж”ҫеӣһж•°з»„гҖӮ
- 移еҠЁеҲ°дёӢдёҖдёӘж•°еӯ—пјҢ并еғҸеңЁдёҠдёҖжӯҘдёӯйӮЈж ·еҶҚж¬ЎжҺ’еәҸпјҢзӣҙеҲ°жІЎжңүж•°еӯ—еү©дёӢгҖӮ
зЁіе®ҡжҺ’еәҸ
дёәдәҶдҪҝз»“жһңжӯЈзЎ®жҺ’еәҸпјҢеҹәж•°жҺ’еәҸеҝ…йЎ»д»ҘзЁіе®ҡзҡ„ж–№ејҸеҜ№е…ғзҙ иҝӣиЎҢжҺ’еәҸгҖӮ
зЁіе®ҡзҡ„жҺ’еәҸз®—жі•жҳҜжҢҮеңЁжҺ’еәҸеүҚеҗҺдҝқжҢҒзӣёеҗҢеҖјзҡ„е…ғзҙ зҡ„йЎәеәҸдёҚеҸҳзҡ„з®—жі•гҖӮеҒҮи®ҫжҲ‘们жңүдёӨдёӘе…ғзҙ "K" е’Ң "L"пјҢе…¶дёӯ "K" еңЁ "L" д№ӢеүҚпјҢдё”е®ғ们зҡ„еҖјйғҪжҳҜ "3" гҖӮеҰӮжһңжҺ’еәҸеҗҺе…ғзҙ "K" д»Қ然еңЁ "L" д№ӢеүҚпјҢеҲҷи®ӨдёәиҜҘжҺ’еәҸз®—жі•жҳҜзЁіе®ҡзҡ„гҖӮ
еҜ№дәҺжҲ‘们д№ӢеүҚеҚ•зӢ¬з ”究зҡ„з®—жі•жқҘиҜҙпјҢи®Ёи®әзЁіе®ҡжҺ’еәҸз®—жі•зҡ„ж„Ҹд№үдёҚеӨ§пјҢеӣ дёәж— и®әе®ғ们жҳҜеҗҰзЁіе®ҡпјҢз»“жһңйғҪжҳҜзӣёеҗҢзҡ„гҖӮдҪҶеҜ№дәҺеҹәж•°жҺ’еәҸжқҘиҜҙпјҢд»ҘзЁіе®ҡзҡ„ж–№ејҸиҝӣиЎҢжҺ’еәҸйқһеёёйҮҚиҰҒпјҢеӣ дёәе…ғзҙ жҜҸж¬ЎеҸӘжҢүдёҖдёӘж•°еӯ—жҺ’еәҸгҖӮ
еӣ жӯӨпјҢеңЁжҢүжңҖдҪҺжңүж•ҲдҪҚеҜ№е…ғзҙ иҝӣиЎҢжҺ’еәҸ并移еҠЁеҲ°дёӢдёҖдёӘж•°еӯ—еҗҺпјҢйҮҚиҰҒзҡ„жҳҜдёҚиҰҒз ҙеқҸд№ӢеүҚеңЁж•°еӯ—дҪҚзҪ®дёҠе·Із»Ҹе®ҢжҲҗзҡ„жҺ’еәҸе·ҘдҪңпјҢиҝҷе°ұжҳҜдёәд»Җд№ҲжҲ‘们йңҖиҰҒзЎ®дҝқеҹәж•°жҺ’еәҸеҜ№жҜҸдёӘж•°еӯ—дҪҚзҪ®д»ҘзЁіе®ҡзҡ„ж–№ејҸиҝӣиЎҢжҺ’еәҸгҖӮ
еңЁдёӢйқўзҡ„жЁЎжӢҹдёӯпјҢеұ•зӨәдәҶеҰӮдҪ•е°Ҷе…ғзҙ жҺ’еәҸеҲ°жЎ¶дёӯгҖӮдёәдәҶжӣҙеҘҪең°зҗҶи§ЈзЁіе®ҡжҺ’еәҸжҳҜеҰӮдҪ•е·ҘдҪңзҡ„пјҢжӮЁиҝҳеҸҜд»ҘйҖүжӢ©д»ҘдёҚзЁіе®ҡзҡ„ж–№ејҸиҝӣиЎҢжҺ’еәҸпјҢиҝҷе°ҶеҜјиҮҙдёҚжӯЈзЎ®зҡ„з»“жһңгҖӮеҸӘйңҖе°Ҷе…ғзҙ д»Һж•°з»„зҡ„жң«е°ҫиҖҢдёҚжҳҜејҖеӨҙж”ҫе…ҘжЎ¶дёӯпјҢе°ұеҸҜд»ҘдҪҝжҺ’еәҸеҸҳеҫ—дёҚзЁіе®ҡгҖӮ
Stable sort?
{{ msgDone }}жүӢеҠЁжј”зӨә
и®©жҲ‘们е°қиҜ•жүӢеҠЁиҝӣиЎҢжҺ’еәҸпјҢд»ҘдҫҝеңЁе®һйҷ…дҪҝз”Ёзј–зЁӢиҜӯиЁҖе®һзҺ°еҹәж•°жҺ’еәҸд№ӢеүҚжӣҙеҘҪең°зҗҶи§Је…¶е·ҘдҪңеҺҹзҗҶгҖӮ
第 1 жӯҘпјҡжҲ‘们д»ҺдёҖдёӘжңӘжҺ’еәҸзҡ„ж•°з»„е’ҢдёҖдёӘз©әж•°з»„ејҖе§ӢпјҢз©әж•°з»„з”ЁдәҺе®№зәіеҜ№еә”еҹәж•°дёә 0 еҲ° 9 зҡ„еҖјгҖӮ
myArray = [ 33, 45, 40, 25, 17, 24] radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
第 2 жӯҘпјҡжҲ‘们д»ҺжңҖдҪҺжңүж•ҲдҪҚејҖе§ӢжҺ’еәҸгҖӮ
myArray = [ 33, 45, 40, 25, 17, 24] radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
第 3 жӯҘпјҡзҺ°еңЁпјҢжҲ‘д»¬ж №жҚ®еҪ“еүҚе…іжіЁзҡ„ж•°еӯ—е°Ҷе…ғзҙ 移еҠЁеҲ°еҹәж•°ж•°з»„дёӯзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮд»Һ myArray зҡ„ејҖеӨҙеҸ–еҮәе…ғзҙ пјҢ并е°Ҷе…¶жҺЁе…Ҙ radixArray дёӯзҡ„жӯЈзЎ®дҪҚзҪ®гҖӮ
myArray = [ ] radixArray = [ [40], [], [], [33], [24], [45, 25], [], [17], [], [] ]
第 4 жӯҘпјҡжҲ‘们е°Ҷе…ғзҙ 移еӣһеҲқе§Ӣж•°з»„пјҢзҺ°еңЁжңҖдҪҺжңүж•ҲдҪҚзҡ„жҺ’еәҸе·Іе®ҢжҲҗгҖӮд»Һ radixArray зҡ„жң«е°ҫеҸ–еҮәе…ғзҙ пјҢ并е°Ҷе…¶ж”ҫе…Ҙ myArray зҡ„ејҖеӨҙгҖӮ
myArray = [ 40, 33, 24, 45, 25, 17 ] radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
第 5 жӯҘпјҡжҲ‘们е°Ҷе…іжіЁзӮ№з§»еҠЁеҲ°дёӢдёҖдёӘж•°еӯ—гҖӮиҜ·жіЁж„ҸпјҢеҖј 45 е’Ң 25 д»Қ然дҝқжҢҒе®ғ们жңҖеҲқзҡ„зӣёеҜ№йЎәеәҸпјҢеӣ дёәжҲ‘们жҳҜд»ҘзЁіе®ҡзҡ„ж–№ејҸиҝӣиЎҢжҺ’еәҸзҡ„гҖӮ
myArray = [ 40, 33, 24, 45, 25, 17 ] radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
第 6 жӯҘпјҡжҲ‘д»¬ж №жҚ®еҪ“еүҚе…іжіЁзҡ„ж•°еӯ—е°Ҷе…ғзҙ 移еҠЁеҲ°еҹәж•°ж•°з»„дёӯгҖӮ
myArray = [ ] radixArray = [ [], [17], [24, 25], [33], [40, 45], [], [], [], [], [] ]
第 7 жӯҘпјҡжҲ‘们д»Һ radixArray зҡ„жң«е°ҫе°Ҷе…ғзҙ 移еӣһ myArray зҡ„ејҖеӨҙгҖӮ
myArray = [ 17, 24, 25, 33, 40, 45 ] radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
жҺ’еәҸе®ҢжҲҗпјҒ
иҝҗиЎҢдёӢйқўзҡ„жЁЎжӢҹпјҢжҹҘзңӢдёҠиҝ°жӯҘйӘӨзҡ„еҠЁз”»жј”зӨәпјҡ
radixArray = [ [
еңЁ Python дёӯе®һзҺ°еҹәж•°жҺ’еәҸ
иҰҒе®һзҺ°еҹәж•°жҺ’еәҸз®—жі•пјҢжҲ‘们йңҖиҰҒпјҡ
- дёҖдёӘеҫ…жҺ’еәҸзҡ„йқһиҙҹж•ҙж•°ж•°з»„
- дёҖдёӘдәҢз»ҙж•°з»„пјҲзҙўеј• 0 еҲ° 9пјүпјҢз”ЁдәҺеӯҳж”ҫеҪ“еүҚдҪҚпјҲеҹәж•°дҪҚпјүеҜ№еә”зҡ„ж•°еҖј
- дёҖдёӘеҫӘзҺҜпјҢе°ҶжңӘжҺ’еәҸж•°з»„дёӯзҡ„ж•°еҖјжҢүеҪ“еүҚеҹәж•°дҪҚж”ҫе…ҘдәҢз»ҙеҹәж•°ж•°з»„зҡ„жӯЈзЎ®дҪҚзҪ®
- дёҖдёӘеҫӘзҺҜпјҢе°Ҷеҹәж•°ж•°з»„дёӯзҡ„ж•°еҖјжҢүйЎәеәҸж”ҫеӣһеҺҹж•°з»„
- дёҖдёӘеӨ–еұӮеҫӘзҺҜпјҢеҫӘзҺҜж¬Ўж•°еҸ–еҶідәҺж•°з»„дёӯжңҖеӨ§еҖјзҡ„дҪҚж•°
жңҖз»Ҳе®һзҺ°зҡ„д»Јз ҒеҰӮдёӢпјҡ
е®һдҫӢ
еңЁ Python зЁӢеәҸдёӯдҪҝз”Ёеҹәж•°жҺ’еәҸз®—жі•пјҡ
mylist = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", mylist)
radixArray = [[], [], [], [], [], [], [], [], [], []]
maxVal = max(mylist)
exp = 1
while maxVal // exp > 0:
while len(mylist) > 0:
val = mylist.pop()
radixIndex = (val // exp) % 10
radixArray[radixIndex].append(val)
for bucket in radixArray:
while len(bucket) > 0:
val = bucket.pop()
mylist.append(val)
exp *= 10
print(mylist)
еңЁз¬¬ 7 иЎҢпјҢжҲ‘们дҪҝз”Ёең°жқҝйҷӨжі•пјҲ"//"пјүеңЁ while еҫӘзҺҜ第дёҖж¬ЎиҝҗиЎҢж—¶е°ҶжңҖеӨ§еҖј 802 йҷӨд»Ҙ 1пјҢдёӢдёҖж¬ЎйҷӨд»Ҙ 10пјҢжңҖеҗҺдёҖж¬ЎйҷӨд»Ҙ 100гҖӮдҪҝз”Ёең°жқҝйҷӨжі•вҖң//вҖқж—¶пјҢе°Ҹж•°зӮ№еҗҺзҡ„д»»дҪ•ж•°еӯ—йғҪдјҡиў«еҝҪз•ҘпјҢ并иҝ”еӣһдёҖдёӘж•ҙж•°гҖӮ
еңЁз¬¬ 11 иЎҢпјҢж №жҚ®еҖјзҡ„еҹәж•°жҲ–еҪ“еүҚе…іжіЁзҡ„ж•°еӯ—еҶіе®ҡе°Ҷе…¶ж”ҫеңЁ radixArray дёӯзҡ„е“ӘдёӘдҪҚзҪ®гҖӮдҫӢеҰӮпјҢеӨ–йғЁ while еҫӘзҺҜ第дәҢж¬ЎиҝҗиЎҢж—¶пјҢexp е°Ҷдёә 10гҖӮеҖј 170 йҷӨд»Ҙ 10 е°Ҷеҫ—еҲ° 17гҖӮ"%10" ж“ҚдҪңйҷӨд»Ҙ 10 并иҝ”еӣһдҪҷж•°гҖӮеңЁиҝҷз§Қжғ…еҶөдёӢпјҢ17 йҷӨд»Ҙ 10 дҪҷ 7гҖӮеӣ жӯӨпјҢеҖј 170 иў«ж”ҫеңЁ radixArray зҡ„зҙўеј• 7 дёӯгҖӮ
дҪҝз”Ёе…¶д»–жҺ’еәҸз®—жі•зҡ„еҹәж•°жҺ’еәҸ
е®һйҷ…дёҠпјҢеҹәж•°жҺ’еәҸеҸҜд»ҘдёҺд»»дҪ•е…¶д»–зЁіе®ҡзҡ„жҺ’еәҸз®—жі•дёҖиө·е®һзҺ°гҖӮиҝҷж„Ҹе‘ізқҖпјҢеҪ“йңҖиҰҒеҜ№зү№е®ҡж•°еӯ—иҝӣиЎҢжҺ’еәҸж—¶пјҢд»»дҪ•зЁіе®ҡзҡ„жҺ’еәҸз®—жі•йғҪеҸҜд»ҘдҪҝз”ЁпјҢдҫӢеҰӮи®Ўж•°жҺ’еәҸжҲ–еҶ’жіЎжҺ’еәҸгҖӮ
д»ҘдёӢжҳҜдҪҝз”ЁеҶ’жіЎжҺ’еәҸеҜ№еҗ„дёӘж•°еӯ—иҝӣиЎҢжҺ’еәҸзҡ„еҹәж•°жҺ’еәҸе®һзҺ°пјҡ
е®һдҫӢ
дҪҝз”ЁеҶ’жіЎжҺ’еәҸзҡ„еҹәж•°жҺ’еәҸз®—жі•пјҡ
def bubbleSort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
def radixSortWithBubbleSort(arr):
max_val = max(arr)
exp = 1
while max_val // exp > 0:
radixList = [[],[],[],[],[],[],[],[],[],[]]
for num in arr:
radixIndex = (num // exp) % 10
radixList[radixIndex].append(num)
for bucket in radixList:
bubbleSort(bucket)
i = 0
for bucket in radixList:
for num in bucket:
arr[i] = num
i += 1
exp *= 10
mylist = [170, 45, 75, 90, 802, 24, 2, 66]
radixSortWithBubbleSort(mylist)
print(mylist)
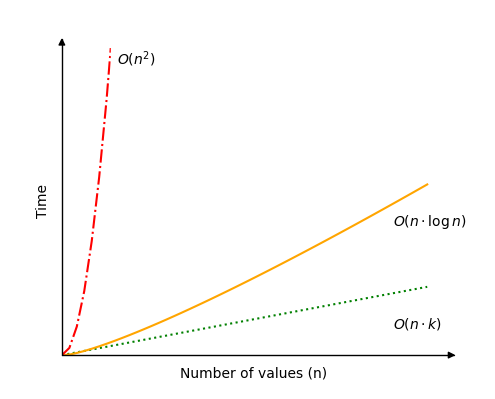
еҹәж•°жҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰ
еҹәж•°жҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰдёәпјҡ\( O(n \cdot k) \)гҖӮ
иҝҷж„Ҹе‘ізқҖеҹәж•°жҺ’еәҸж—ўеҸ–еҶідәҺйңҖиҰҒжҺ’еәҸзҡ„еҖј \(n\)пјҢд№ҹеҸ–еҶідәҺжңҖй«ҳеҖјдёӯзҡ„ж•°еӯ—дҪҚж•° \(k\)гҖӮ
еҹәж•°жҺ’еәҸзҡ„жңҖдҪіжғ…еҶөжҳҜпјҢеҰӮжһңжңүеӨ§йҮҸеҖјйңҖиҰҒжҺ’еәҸпјҢдҪҶиҝҷдәӣеҖјзҡ„ж•°еӯ—дҪҚж•°еҫҲе°‘гҖӮдҫӢеҰӮпјҢеҰӮжһңжңүи¶…иҝҮдёҖзҷҫдёҮдёӘеҖјйңҖиҰҒжҺ’еәҸпјҢдё”жңҖй«ҳеҖјдёә 999пјҢеҸӘжңүдёүдҪҚж•°еӯ—гҖӮеңЁиҝҷз§Қжғ…еҶөдёӢпјҢж—¶й—ҙеӨҚжқӮеәҰ \(O(n \cdot k)\) еҸҜд»Ҙз®ҖеҢ–дёә \(O(n)\)гҖӮ
еҹәж•°жҺ’еәҸзҡ„жңҖеқҸжғ…еҶөжҳҜпјҢеҰӮжһңжңҖй«ҳеҖјдёӯзҡ„ж•°еӯ—дҪҚж•°дёҺйңҖиҰҒжҺ’еәҸзҡ„еҖјж•°йҮҸзӣёеҗҢгҖӮиҝҷеҸҜиғҪдёҚжҳҜдёҖдёӘеёёи§Ғзҡ„жғ…еҶөпјҢдҪҶеңЁиҝҷз§Қжғ…еҶөдёӢпјҢж—¶й—ҙеӨҚжқӮеәҰе°ҶжҳҜ \(O(n^2)\)гҖӮ
жңҖе№іеқҮжҲ–жңҖеёёи§Ғзҡ„жғ…еҶөеҸҜиғҪжҳҜпјҢеҰӮжһңж•°еӯ—дҪҚж•° \(k\) зұ»дјјдәҺ \(k(n)= \log n\)гҖӮеҰӮжһңжҳҜиҝҷж ·пјҢеҹәж•°жҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰдёә \(O(n \cdot \log n )\)гҖӮдҫӢеҰӮпјҢеҰӮжһңжңү 1000000 дёӘеҖјйңҖиҰҒжҺ’еәҸпјҢдё”иҝҷдәӣеҖјжңү 6 дҪҚж•°еӯ—гҖӮ
иҜ·еҸӮи§ҒдёӢеӣҫдёӯзҡ„еҹәж•°жҺ’еәҸзҡ„дёҚеҗҢеҸҜиғҪж—¶й—ҙеӨҚжқӮеәҰгҖӮ